Abstract
Purpose: Providing vision correction in communities where healthcare facilities are unavailable is problematic. Here, we explore the possibility of using pinholes as near visual aids in the developing world.
Method: Uncompensated (without the pinhole) proximal visual acuities (VAs) were measured and recorded for one eye of 45 presbyopic subjects over the age of 50 years in photopic (250 lux) and scotopic (20 lux) conditions. The proximal VAs were then repeated while the subjects looked through nine different pinholes.
Results: The VAs varied with the diameter of each pinhole. A comparative measure was devised to determine the relative performance of different diameter pinholes as a near visual aid. The results suggest an improvement of more than 40% in VA in about 67% of subjects in good lighting conditions and about 60% in poorer lighting conditions.
Conclusion: By creating more awareness that there are other ways of improving vision that cost almost nothing, visual impairment can be reduced until spectacles become available.
Introduction
The world population in 2016 is approximately 7.3 billion.1 There are approximately 45 million blind people worldwide and an additional 180 million people with low or impaired vision.2 There are between 800 million and 2.3 billion people with refractive error, but only 1.8 billion have access to vision correction, leaving approximately 500 million with uncompensated refractive errors (UREs).3 Worldwide, URE is the most common cause of vision impairment after cataracts.3 With the global population growing at a rapid rate and life expectancy also increasing, the above-mentioned figures for URE are likely to increase.3
Presbyopia also creates a refractive error affecting near vision of older people, and yet it is not included in the World Health Organization’s reported prevalence of uncorrected refractive error.3 It affects approximately 1 billion people, of whom about 517 million do not have adequate near-vision correction. Functional or significant near-vision impairment (defined as adding sufficient plus dioptric power correction to the distance refractive correction to achieve the correct near-vision criterion) is experienced by about 410 million people. Sixty-seven percent of people with presbyopia and 94% of people with functional or significant near-vision impairment because of uncorrected presbyopia live in developing countries. Combining the prevalence data with the population growth gave an estimate of 1.04 billion cases of functional presbyopia in 2005. The global prevalence of presbyopia is predicted to increase to about 1.4 billion in 2020 and to about 1.8 billion by 2050.4
In most developed countries, the optometrist to population ratio is approximately 1:10 000. However, in developing countries, the ratio is far greater (approximately 1:600 000), and much worse in many rural areas, with up to millions of people per optometrist.4 This lack of eye-care practitioners is the main reason for the high rates of vision problems that are because of uncorrected refractive error in developing countries. In order to deliver quality eye care to countries where the need is the greatest, a substantial increase in the number of eye-care personnel trained in refraction is needed. The present situation in many developing countries cannot wait for optometry to develop completely as a profession, but requires local healthcare services to take a major role in training mid-level personnel in refraction and eye care.4 Smith et al.5 show the potential loss in productivity because of visual impairment globally to be about $268.8 billion. The cost of providing spectacles to meet this global demand is unknown. If it is assumed that spectacles are replaced at a rate of one pair every 3 years, 53 million spectacles would be needed annually to address the current problem of uncorrected refractive error. While the financial cost of providing the spectacles alone is considerable, the time, labour and infrastructure cost of providing such visual aids is no less considerable. But, if an uncompensated ametrope or presbyope pricks a small hole into a leaf, piece of paper or cardboard and looks through it, he will usually experience improved vision providing there is no central cataract or any ocular pathology. Similarly, individuals in such circumstances could improve their vision by looking through a small hole while reading. The question is: Could such a simple and almost cost-free device contribute to solving this need?
The purpose of this study was to examine and determine the effect of pinhole size on near or proximal visual acuity (VA) and determine the viability of pinholes as a visual aid for the presbyopic population in photopic and scotopic conditions. We emphasise that the use of a pinhole is not a substitute for an eye test or for a pair of spectacles, but note its utility as a temporary measure to improve vision where eye care or spectacles are not readily available.
Data acquisition
Any willing participant, provided he or she was 50 years of age or older, was allowed to participate in the study. All subjects who participated in the study were made aware of the purpose and methodology, and consent was obtained from each participant by means of a signed consent form. All investigations and measurements performed in this study adhered to the rules and regulations of the Declaration of Helsinki and were approved by the Ethics Committee of the Faculty of Health Sciences of the University of Johannesburg.
Uncompensated near or proximal VAs were measured on the participant eye that gave the best VA of 45 presbyopic subjects over the age of 50 years in photopic (250 lux) and then scotopic (20 lux) conditions. Subjects (and ages) were chosen arbitrarily. There were 36 male and 9 female subjects. Their ages ranged between 50 and 74 years with an average of 59 years (standard deviation = 7.52 years). The room illumination for photopic conditions was measured using a Sekonic Lumi Model 246 light-metre. No visual or pathological conditions or requirements were set for the subjects. The subjects were asked to read the smallest letters on a near-VA chart by moving the chart closer or further away from their eyes at the distance that gave the best acuity. The chart used was the Lighthouse Near Visual Acuity Test (second edition) with modified Early Treatment For Diabetic Retinopathy Study Sloan letters. VA measurements were then repeated and recorded while the subjects looked through nine pinholes of different diameters, one at a time. The diameters were 0.6 mm, 1.0 mm, 1.2 mm, 1.5 mm, 2.0 mm, 2.5 mm, 3.0 mm, 3.5 mm and 4.0 mm. The pinholes were drilled through plastic occluders of 1-mm thickness by Technical Services of the University of Johannesburg. Four different Lighthouse Near Visual Acuity charts with different letters were used randomly while looking through the different size pinholes to prevent the subjects from memorising the letters. The same procedure was repeated for scotopic conditions. An ordinary white candle was used to simulate scotopic conditions as used by people who do not have any electricity and use candles as their only source of light. The candle was lit in a completely dark room and placed next to the chart. The light-metre was then placed on the chart and an illumination of 20 lux was recorded. In order to record consistent scotopic VA measurements, a lamp with a rheostat on the switch to adjust the light intensity, was used to illuminate the chart to 20 lux and used for each subject. The surrounding lighting condition for scotopic conditions in the test room was not uniform, but only 20 lux reflecting off the chart. All tests were performed in the same room maintaining identical settings to avoid external distractions. Each subject spent approximately 25–30 min doing the study.
The VAs measured were converted to minimum angles of resolution (MARs). MARs were used for data analysis because MAR has limits and these limits have physical meaning. Physiologically, the visual field of a single human eye is about 150° laterally and about 125° vertically. The smallest angle resolvable by the human eye is less than 1′ but greater than zero.6 An MAR of zero is not achievable because this corresponds to perfect resolution of zero-size objects at an arbitrary large distance. Similarly, an MAR of 150° or greater corresponds to an inability to discern objects which span the entire visual field. One might consider such a condition as a definition of total blindness. One can perform a statistical analysis with MAR in a well-defined way, and the smaller the MAR of a subject, the greater amount of detail discernible, hence the better the VA of the subject. We define MAR as:
where d is the distance from the chart that gave the best resolution for the smallest letters read and M is the M-value of the smallest line of letters read on the chart.
The VAs measured where pinholes were used as visual aids shall be referred to as compensated VAs, while those measured without use of visual aids shall be referred to as uncompensated VAs in what follows. We note that this is somewhat unconventional usage because the refractive errors are not compensated.
The behaviour of a pinhole as an optical system is determined by the diameter of the pinhole. As such, the effect of a pinhole on VA is dependent on the size of the pinhole. We would like to determine the relative performance of pinholes of different sizes on VA. An objective measure is required to perform such a comparison. VAs and changes in VA are subjective measurements. A method to make objective analysis of this data is presented in the next section.
Data analysis
Two separate, yet related, analyses were conducted, a conservative measurement and an adjusted measurement analysis. Each complete row of letters on the near-test chart corresponds to an M-value and there are five letters per line. For the conservative measurement, the subject was asked to read as many letters as possible on the chart at any distance that gives the best acuity. The M-value of the last complete line read on the near chart was recorded and the MAR computed. If they could not read the entire line, then they did not resolve that angle. For the adjusted measurement, if all the letters are read on a particular line and n on the next is computed, that includes the last n letters.
Compensated or aided values were subtracted from uncompensated values. Given an unaided MAR θi and an aided  , of a given pinhole, for a subject i we define the difference in MAR as: , of a given pinhole, for a subject i we define the difference in MAR as:
In this way, positive Δθi corresponds to improvement in VA and negative Δθi corresponds to a deterioration in VA when using a particular pinhole. When Δθi is zero, there is no change in VA. Difference MAR values were computed for conservative and adjusted measurements in both photopic and scotopic conditions. Similarly, differences in letter counts were computed. However, the improvements in letter counts show negative values, while positive values show deterioration.
We define, for a given pinhole, the mean difference  as: as:
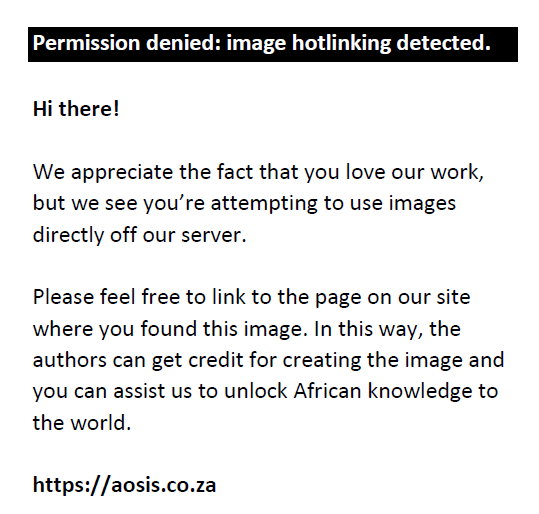
where Δθi is the difference in MAR of subject i using the given pinhole in a group of N subjects. Mean differences in MAR were calculated for conservative and adjusted measurements. The relative performance of a pinhole as a visual aid is determined by computing the fractional difference ΔΘi in VA when using that given pinhole as a visual aid versus the unaided VA:
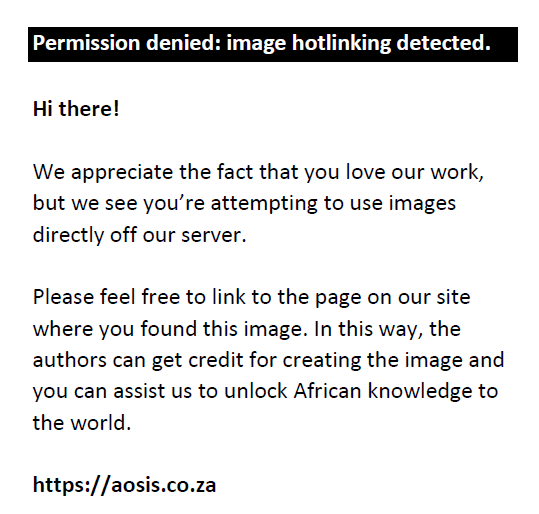
Conservative and adjusted fractional difference MAR values were computed for each pinhole over all subjects. We define the mean fractional differences MAR for a given pinhole over all N subjects as:
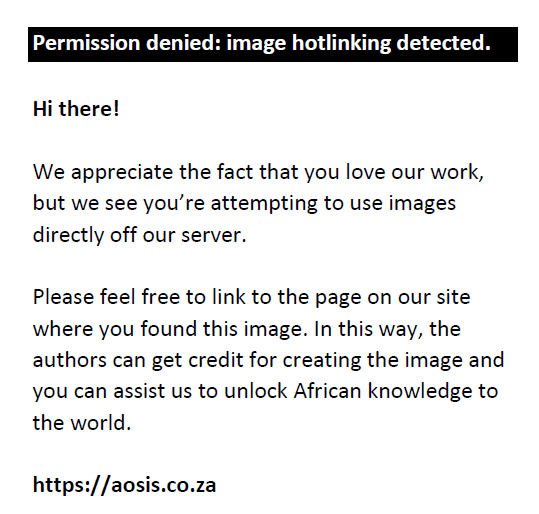
Again, conservative and adjusted mean fractional difference MAR values were computed for each pinhole over all subjects.
We compute fractional differences to remove baseline values from the data. They are measures characterised by unitless numbers. It is these properties that make the fractional difference a useful measure by which we quantify change. For example, four subjects, 1, 2, 3 and 4, have uncompensated MARs of θ1, θ2, θ3 and θ4, respectively. If the computed MAR mean fractional difference value for the four subjects is 0.5% or 50%, then subjects 1, 2, 3 and 4 will each experience a 50% change in MAR on average. A fractional difference of 0 means no change in MAR. A positive value is an improvement while a negative value indicates deterioration. Fractional differences will never reach a value of 1 because that would imply an unrealistic 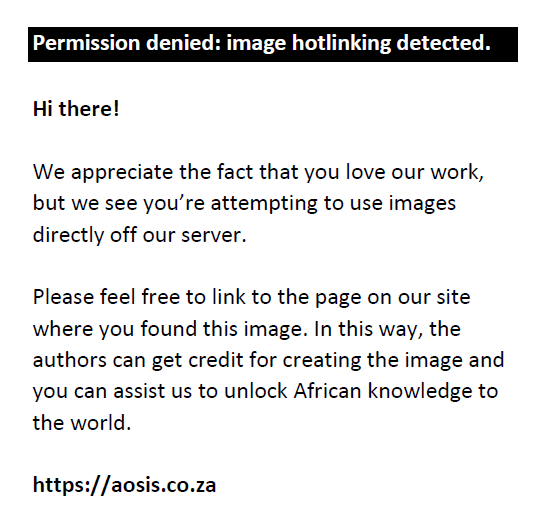 of 0.0. For this study, we are only interested in mean fractional difference MAR. Next, we present results of the analysis presented above. of 0.0. For this study, we are only interested in mean fractional difference MAR. Next, we present results of the analysis presented above.
Results
Not every subject’s MAR or VA improved while looking through the pinholes. Some subjects may have had some form of pathology, and the mean results obtained may not give a true reflection of the potential effect the pinhole may have on vision. So the numbers were reworked on a subset of the subjects that showed improvement. Table 1 shows the number of subjects and percentages of the 45 subjects where MARs did improve through the respective pinhole diameters. Tables 2 and 3 show the mean values for photopic conservative and adjusted measurements, respectively, with mean fractional difference MAR and standard deviations. Tables 4 and 5 present the mean values for scotopic conservative and adjusted measurements, respectively, and with a mean fractional difference MAR and standard deviations.
| TABLE 1: The number (n) and percentage of subjects where visual acuity improved through the various pinhole diameters. |
| TABLE 2: Mean values for improved photopic conservative conditions. |
| TABLE 3: Mean values for improved photopic adjusted conditions. |
| TABLE 4: Mean values for improved scotopic conservative conditions. |
| TABLE 5: Mean values for improved scotopic adjusted conditions. |
For conservative photopic conditions, the 2.0-mm-diameter pinhole showed the best mean fractional difference MAR of 0.457 (±0.22) followed by the 1.0-mm-diameter pinhole [0.452 (±0.2)] and then the 1.5-mm-diameter pinhole [0.449 (±0.23)], respectively (see Table 3). The adjusted mean fractional difference results showed the 1.5-mm-diameter pinhole [0.450 (±0.22)] to be best followed by the 1.2-mm-diameter pinhole [0.432 (±0.24)] and then the 1.0-mm-diameter pinhole [0.431 (±0.22)], respectively (see Table 4).
For conservative scotopic conditions, the 1.0-mm-diameter [0.415 (±0.24)] pinhole showed the best mean fractional difference MAR improvement followed by the 1.5-mm-diameter pinhole [0.413 (±0.20)] and then the 0.6-mm-diameter pinhole [0.399 (±0.24)], respectively (see Table 5). The adjusted mean fractional difference MAR measurements showed the 1.5-mm-diameter pinhole [0.417 (±017)] to be the best followed by the 1.0-mm-diameter pinhole [0.401 (±0.27)] and then the 1.2-mm-diameter pinhole [0.363 (±0.21)], respectively (see Table 6). A summary of the results for the best three pinhole diameters showing the best fractional difference MARs is shown in Table 6.
| TABLE 6: Summary of results obtained for the three pinhole diameters that gave the best fractional difference minimum angle of resolution improvements for all subjects. |
The 2.0-mm-diameter pinhole showed the best fractional difference MAR improvement (0.457) for conservative photopic conditions followed by the 1.0-mm-diameter pinhole (0.452) and then the 1.5-mm-diameter pinhole (0.449), respectively. The 1.5-mm-diameter pinhole (0.450) showed most improvement for adjusted measurements followed by the 1.2-mm-diameter pinhole (0.432) and then 1.0-mm-diameter pinhole (0.431), respectively. The conservative photopic measurements showed the greater mean improvement of 0.457 (2.0 mm pinhole) when compared with the adjusted measurements, which were slightly less with a mean improvement of 0.450 (1.5-mm-diameter pinhole).
One would have expected the adjusted measurements to show a larger improvement as more letters were read. The scotopic results, however, showed the adjusted measurements to be better. The 1.5-mm diameter pinhole showed the best with 0.417 when compared with the conservative result of 0.415 from the 1.0-mm-diameter pinhole. The relative performance of each pinhole is not directly observable from these results. Further analysis is required to make meaningful objective comparison of relative performance of different pinholes on VA. This analysis, and a discussion thereof, is presented next.
Fitness function and pinhole rank
The pinhole diameter that shows the largest mean fractional difference MAR improvement may not always be the best choice to help a large population. That particular pinhole may show the largest mean fractional difference MAR improvement; however, it may help fewer subjects. Therefore, a fitness rating is determined for each pinhole size to determine which diameter provided the best all-round performance. The purpose of a rating for each pinhole is to determine which pinhole diameter performed the best overall. The aim is to build a function such that we penalise the pinholes that perform poorly and reward the ones that perform well. Well-performing pinhole diameters make significant improvements in VA and help many people. Poor performing pinholes make insignificant changes in VA or help only a small fraction of people. However, a poor performing pinhole may make a significant improvement in VA, but may help only a few subjects to see better.
The fitness rating comprises two variables, fractional difference MAR y and the fraction of subjects who showed improvement n. The fitness rating is defined by:
If n and y are both small, f is small. If one parameter is large and the other is small, then f is also small. Similarly, if n and y are large, f will be large. The function must be symmetrical and a product of n and y is required because an addition or division of the two will not punish the poor performing pinhole diameters. The logarithm of ny will be negative so the negative of the logarithm is taken to give a positive f. The fitness ratings are derived data contained in Table 1, showing the number of people that each pinhole helped to see better, and Tables 2–5 show the fractional difference MAR values for each pinhole in each lighting condition. The associated fitness ratings are presented in Table 7.
The 2.0-mm-diameter pinhole produced the highest mean fractional difference MAR improvement (0.457), followed by the 1.0-mm-diameter (0.452) and then the 1.5-mm-diameter pinhole (0.449) for photopic conservative conditions. The 1.2-mm-diameter pinhole, which had the fourth highest mean fractional difference MAR of 0.438, produced the best overall performance by helping a greater percentage of the subjects (67%), followed by the 1.5-mm-diameter pinhole (62%) and only then the 2.0-mm-diameter pinhole (56%). The mean fractional difference MAR of the 1.2-mm-diameter pinhole was slightly less (0.438) than the 2.0-mm-diameter pinhole (0.457); however, on average, it improved the VA of more subjects. The 1.0-mm-diameter pinhole, however, showed the second highest mean fractional difference MAR of 0.452, but only improved the VA of 38% of the subjects. The 1.0-mm-diameter pinhole finished fifth in the ratings behind the 2.5-mm-diameter pinhole, which had a mean fractional difference MAR improvement of 0.401, but helped 47% of the subjects.
For photopic adjusted conditions the 1.2-mm-diameter pinhole (0.432) also performed the best followed by the 1.5-mm-diameter pinhole (0.450) and then the 2.0-mm-diameter pinhole (0.406), although the 1.5-mm-diameter pinhole showed a higher mean fractional difference MAR. The 1.2-mm-diameter pinhole on average improved the VA of 67% of the subjects followed by the 1.5-mm-diameter pinhole (62%) and then the 2.0-mm-diameter pinhole (60%). The 1.0-mm-diameter pinhole showed a mean fractional difference MAR improvement of 0.431 that was higher than the 2.0-mm-diameter pinhole (0.406); however, it only helped 40% of the subjects. The 1.0-mm-diameter pinhole also finished fifth in the rankings behind the 2.5-mm-diameter pinhole, which had a mean fractional difference MAR of only 0.342; however, the pinhole improved the VA of 56% of the subjects.
For scotopic conservative conditions, the 1.5-mm-diameter pinhole performed the best followed by the 1.2-mm-diameter and then the 2.0-mm-diameter pinhole. The 1.5-mm--diameter pinhole, however, had a lower mean fractional difference MAR (0.413) than the 1.0-mm-diameter pinhole (0.415), but on average improved the VA of 62% of the subjects compared to only 38% from the 1.0-mm-diameter pinhole. The 1.0-mm-diameter pinhole, however, was not among the top three ratings. The 1.2-mm-diameter pinhole also improved 67% of the subjects’ VA but had a mean fractional difference MAR of only 0.357. The 2.0-mm-diameter pinhole had a mean fractional difference MAR of only 0.333, but improved 56% of the subjects VA. The 3.0-, 3.5- and 4.0-mm-diameter pinholes performed better than the 0.6-mm and 1.0-mm-diameter pinholes. The larger pinhole diameters rated slightly higher when compared with photopic conditions.
For the adjusted scotopic measurements, the 1.5-mm-diameter pinhole also performed the best followed by the 1.2-mm-diameter and the 2.0-mm-diameter pinholes. The 1.5-mm-diameter pinhole also had the best mean fractional difference MAR (0.417) and improved the VA of 53% of the subjects. The 1.2-mm-diameter pinhole, however, improved the VA of 58% of the subjects but had a mean fractional difference MAR of only 0.363. The 2.0-mm-diameter pinhole had a mean fractional difference MAR of 0.316 and also improved the VA of 58% subjects. The 2.5-mm-diameter (0.322) and 3.0-mm-diameter (0.348) pinholes showed better mean fractional difference MARs; however, both pinholes improved only 51% of the subjects VA. The 3.5-mm-diameter pinhole improved the VAs of 56% of the subjects; however, the mean fractional difference was only 0.294. The 4.0-mm-diameter pinhole improved 38% of the subjects VAs; however, it showed the lowest mean fractional difference improvement of only 0.290.
Discussion
It can be seen that the pinhole diameter that produces the highest mean fractional difference MAR is not necessarily always the diameter of choice. The best pinhole depends on what it is used for. This study suggests that if a community health worker were to go into the rural area and help the community see better, the 1.2-mm diameter would be the diameter of choice for photopic conditions and 1.5-mm diameter for scotopic conditions. Those diameters may not have given the largest mean fractional difference MAR improvement; however, these diameters on average helped a greater number of people see better.
The three pinhole diameters that performed best for both photopic and scotopic conditions all showed mean fractional difference MAR improvements greater than 0.4. That means that the population discussed will, on average, obtain at least a 40% improvement in MAR. For example, a subject with an uncompensated MAR of 5′ (6/30) may obtain a 2′ MAR improvement giving a VA of 6/18. Another subject may have an uncompensated MAR of 6′ (6/36). A 40% improvement gives a 2.4′ improvement giving a compensated MAR of 3.6′ (6/21.60 ≈ 6/24). For large populations, if a decision had to be made on which size pinhole would perform the best, the pinhole diameter that shows the highest mean fractional difference MAR improvement may not always be the best choice. That particular pinhole may show the greatest VA improvement; however, it may not have helped the most people. There is enough evidence to show that by looking through a pinhole vision usually improves. The pinhole is used as a diagnostic tool in optometry and ophthalmology. Ophthalmology is implanting pinhole corneal inlays to improve vision and optometrists are experimenting with pinhole contact lenses.7,8,9
Of course, a pinhole is no substitute for an eye test or a spectacle lens or any optometric, ophthalmological or other health service. It is certainly not a sufficient solution to the visual needs of the developing world; but the huge potential benefit strongly suggests that there is a niche for it. One imagines that implementation could be applied in communities where there are no or almost no health services and that it could be used to increase awareness of the fact that vision can be aided and eventually help to feed people into orthodox optometric and ophthalmological services. The results suggest that so simple a device as a pinhole can improve the near vision of about 67% of people over 50 years of age in good lighting conditions and, perhaps, about 60% in poor lighting conditions. The potential benefit is so great and the cost so little that it is surely negligent not to explore the possibility of developing such a programme.
Thus, VA can be improved simply by looking through a small hole, and simple pinholes will have some impact on people suffering from visual impairment, especially for those who cannot afford spectacles and for people in remote areas where no eye care is available. If a pinhole is used as a diagnostic tool for vision screenings, why not make people aware of it especially for those who cannot afford spectacles? A small hole in a piece of paper or leaf costs absolutely nothing. The objective would not be to substitute the pinhole for spectacles, but only to improve VA in the interim until affordable spectacles are available. The point here is awareness. A disadvantage is that it may be uncomfortable holding a pinhole in front of the eye for long periods of time while looking at distant or near targets. Pinhole spectacles are available, which may overcome the problem of monocular viewing. Although the purpose of this study is not to promote pinhole spectacles, such spectacles may be another option for those who can afford proper ones. They are based on the same pinhole optics principle. The advantage of these spectacles is that no distortion effects such as pincushion and barrel distortion are observed because there is no refraction. Spherical aberration is reduced because of the smaller diameter pupil; however, visual fields are restricted.
People who have had corneal surgery or keratoconus may find that their vision cannot be completely corrected with spectacle lenses and may find that looking through a pinhole or pinhole spectacles improves their vision. Pinhole spectacles have also been shown to improve the VA of people who have cataracts.10 Pinholes, however, do not improve vision if the VA is very close to 6/6. Diffraction effects occur and VA decreases. Pinhole spectacles may be more efficient than holding a single pinhole and looking through it. Performing near tasks, however, may also be difficult while at the same time trying to hold a single pinhole. The real vision problem lies with the under-privileged and rural population. They would soon realise that poor vision is not inevitable and this may bring many more into the conventional system. The same applies to cataracts. Many people do not realise that cataracts can be extracted and replaced by intraocular lenses. Under certain circumstances, people may be left aphakic, but vision can be restored with spectacles or, if left uncompensated, VA can be improved by means of a pinhole. By creating more awareness that there are other ways of improving vision that cost almost nothing, visual impairment can be reduced until spectacles become available.
Limitations
Many measurements were recorded on each subject, and fatigue may have had an influence on some measurements. The sample size was small. Although the idea was to examine all subjects unconditionally, perhaps they should have been screened for pathology so that a larger sample size could have been obtained. The lighting conditions under scotopic conditions were only 20 lux reflecting off the chart. This may have influenced some of the measurements as some subjects may have had better illumination by moving closer to the chart while reading (the inverse square law11). The idea of the study was to simulate conditions experienced by subjects who do not have electricity and their only source of light being a candle. Another study could be done with the ambient lighting being constant for all conditions; however, natural conditions would then no longer be being simulated.
Conclusion
We submit that the pinhole does have potential as a visual aid in the developing world. It does not replace spectacles but can serve until spectacles become available. Much could be done with very little cost.
Acknowledgements
Competing interests
The authors declare that they have no financial or personal relationships which may have inappropriately influenced them in writing this article.
Authors’ contributions
A.S.C. did the bulk of the research for the M.Phil. degree under the guidance of W.F.H. W.A.C. assisted with the analysis.
References
- Current World Population [homepage on the Internet]. [cited 2015 Nov 15]. Available from: http://www.worldometers.info/world-population/
- Berger I, Dunnaway D, Mistry K. Worldwide distribution of visual refractive errors and what to expect at a particular location. Conference: Affordable Vision Correction; Clarendon Laboratary Hall; University of Oxford; 7–9 August 2004; Oxford.
- Holden BA, Fricke T, May S, et al. Global vision impairment due to uncorrected presbyopia. Arch Ophthalmol. 2008;126:1731–1739. http://dx.doi.org/10.1001/archopht.126.12.1731
- Holden BA, Resnikoff S. The role of optometry in Vision 2020. Community Eye Health J. 2002;15(43):33–36.
- Smith TST, Frick KD, Holden BA, et al. Potential loss productivity resulting from the global burden of uncorrected refractive error. Bull World Health Org. 2007;87: 431–437. http://dx.doi.org/10.2471/BLT.08.055673
- Grosvenor T. Primary care optometry. 3rd ed. Butterworth-Heinemann; Singapore; 1996.
- Waring G. Corneal inlay uses pinhole effect. Ophthalmology Times. 2010;35;7.
- Seyeddain O, Riha W, Hohensinn M, et al. Refractive surgical correction of presbyopia with the Acufocus small aperture corneal inlay: Two-year follow-up. J Ref Surg. 2010;26:707–715. http://dx.doi.org/10.3928/1081597X-20100408-01
- García-Lázaro S, Ferrer-Blasio T, Radhakrishnan H, et al. Visual function through 4 contact lens-based pinhole systems for presbyopia. J Cat Ref Surg. 2012;38:858–865. http://dx.doi.org/10.1016/j.jcrs.2011.11.042
- Baraldi P, Enoch JM, Raphael S. Vision through nuclear and posterior subcapsular cataract. Inter Ophthalmol. 1986;9:173–178. http://dx.doi.org/10.1007/BF00159846
- Meyer-Arendt JR. Introduction to classical and modern optics. 3rd ed. Engelwood-Cliffs NJ: Prentice Hall Inc; 1989.
|