Wavefront aberrations can be described as deviations of the wavefront exiting the eye from a reference wavefront that is aberration free and diffraction limited. Ocular aberrations can be sub-categorised as lower and higher order aberrations. Ocular aberrations have prompted interest amongst the ocular healthcare community owing to their influences on the visual functioning of patients as well as differences observed in ocular aberrations through the use of refractive surgery both pre- and post-operatively. Uncompensated refractive error remains one of the most common reasons for which patients consult optometrists. Compensation of refractive error, or lower order aberrations, has become a routine procedure during an optometric examination. However, there are some patients who experience visual symptoms even after their refractive errors have been compensated via spectacles or contact lenses. Higher-order aberrations may be the source of these visual disturbances. Refractive surgery has been found to influence and even induce various changes in higher-order aberrations post-operatively, which in turn has led to increased interest in wavefront aberrations and how the measurement of these aberrations can improve diagnosis and treatment within optometry and ophthalmology.

Vergence, with regard to wavefront optics, is the term used to describe the curvature of a diverging (leaving a point source) or a converging (going towards a point source) wavefront.¹ Vergence, portrayed as travelling wavefronts, has allowed the development and use of wavefront error analysis in optometry and ophthalmic surgery.²

Wavefront aberrations refer to the deviations of a wavefront exiting the pupil after progressing through the optics of the tested eye when compared to a reference wavefront that is aberration free.^2,3 Wavefront aberrometers are the instruments used to measure the above-mentioned aberrations as well as relevant variables such as pupil size.⁴ Wavefront aberrometers utilise wavefront analysis to determine the refractive parameters of the eye as well as the groups of aberrations classified as either lower or higher order aberrations.²

The technological advances in wavefront aberrometry have allowed for a deeper understanding of aberrations and more accurate compensation of such aberrations by means of refractive surgery or other methods such as custom-designed contact lenses. The eye, being a flawed optical system, has numerous aberrations such as coma and spherical aberrations.³

Aberrometers typically send monochromatic light rays into the eye, through the pupil, and the rays are reflected back off the fundus. In a perfect optical system, the light rays that emerge from the eye would be parallel and an undistorted plane wavefront would be formed.³ However, in human eyes, the information that reaches the photosensors of the instrument is a reflection of both diffraction and the imperfections of the optical components within the eye and, via calculations, it is possible to describe the distortions of the wavefront in the entrance pupil of the eye.³

Ocular aberrations, as mentioned above, are deviations of the wavefront exiting the eye from a chosen unaberrrated reference wavefront³ and can be affected by many variables that would influence the measurement taken. Such variables for a particular eye can include tear film stability,⁵ lid position,⁶ pupil size, accommodation⁷ and fixational eye movements,⁸ to name a few.

The tear film is composed of three layers (i.e. the aqueous layer, lipid layer and mucin layer) and is the first ocular structure that a progressing wavefront comes into contact with on its passage into the eye. Changes in the tear film composition or viscosity can alter the stability and thickness of the tears and, hence, can modify the optical quality of the eye’s front surface, which in turn can influence ocular aberrations.⁵ Previous studies have shown that the tear film is dynamic and wavefront aberrations will change as the tear layer does.⁵ It has been demonstrated that tear film instability causes an increase in ocular aberrations.⁵

Prolonged lid pressure has the ability to induce topography changes to the corneal surface.⁶ Previous studies have indicated that lower and higher order aberrations can be altered by the lid position during near work.⁶ Wavefront errors seem to correlate with the position of the lid during the near task.⁶ The aberrations most influenced by near work are defocus and astigmatism . During reading, it was noted that a small defocus shift in the hyperopic direction occurred most frequently.⁶

The pupil size of healthy patients generally fluctuates with light and accommodation (near triad) throughout the day. The pupil diameter therefore influences the retinal image in terms of luminance and depth of focus and field. Pupil constriction causes a decrease in retinal luminance; however, a smaller pupil affords an increase in depth of field and focus. The diameter of the pupil also influences diffraction and thus image quality.⁷ Pupil diameter and the extent of diffraction have an inversely proportional relationship.⁷ Aberrations can, at times, be minimised by miosis; however, this also increases the effects of diffraction and thus decreases retinal image quality and visual resolution. Higher order aberrations are often affected by pupil size. When performing measurements for laboratory use, the iris sphincter and ciliary muscle are often paralysed using cycloplegics, to inactivate pupillary oscillations and accommodation⁹ to ensure the validity of measurements.

Accommodation (the eye’s ability to change the refracting power of the internal crystalline lens) allows accurate focusing of objects at varying distances. The eye houses the crystalline lens as well as the muscle that controls accommodation.⁷ The ciliary muscle governing the accommodative actions contracts whilst the lens zonules relax, which allows greater lens convexity, thereby increasing the refractive power of the eye. The above-mentioned muscle action allows the clear viewing of proximal objects. The change that the lens undergoes is roughly spherical in the absence of other variables.⁷ Accommodation for proximal objects forms one part of the so-called near triad, with the other two entities being convergence and miosis.⁷ Refractive state can be determined both objectively (examiner or instrument dependent) or subjectively (patient response dependent). However, it remains imperative that the accommodative system is fully relaxed as active accommodation can hinder the accuracy of the refractive error or lower order aberration measurement.¹⁰

Fixational eye movements, being both voluntary and involuntary, can influence the measurements of ocular aberrations. When a patient fixates an object, small eye movements occur (of which the patient is unaware) including drifts, tremors and microsaccades. As aberrations are measured with reference to a chosen or reference plane wavefront, that is undistorted, any eye movement would further shift the measured wavefront error closer to or further away from the reference wavefront and thus change the value of the Zernike coefficients .⁸

Polynomials are mathematical equations that usually involve multiple terms and variables.¹¹ Zernike polynomials are one of the mathematical representations that can be used to describe wavefront errors. The variables found in the expressions of Zernike polynomials describing the wavefront (W) are the Greek symbol rho (ρ), and the angle theta (θ), measured as a deviation from the reference horizontal meridian. Rho can further be defined as the distance from the chosen point to the center of the pupil (r) divided by the radius of the exit pupil (a or r_max).¹² This method of representing the variables is known as the spherical polar system and is represented as a polar coordinate pair, written as (ρ; θ).¹²

Zernike polynomials are advantageous when describing the wavefront error as their notation is specific to the aberrations they are classifying and can be expressed using either a single (Z_j) or double indexing method system. The single index (usually as j) is perhaps simpler but the double indexing method allows the representation of more information in one term. The double indexing system displays both the order (n) and frequency (m) of the wavefront error.¹³ This method of Zernike expression also allows easier comparison of wavefront errors as aberrations with the same frequency have similar shapes.¹³ Single and double index systems can be used interchangeably and the sub- and superscripts can be converted using an equation. For example, to convert the double indexing system to a single indexing, the following equation is used:¹³

whereby n is the radial order and m is the frequency.

The information from the wavefront aberrometer can also be given in the form of Zernike coefficients that reflect the same order and frequency as the corresponding Zernike polynomials, measured in micrometers (μm).¹³

The use of Zernike polynomials is beneficial as they possess a certain set of properties that allows them to be used somewhat universally.¹³ The fact that these polynomials are orthonormal allows the researcher to limit the expansion (i.e., only work with aberrations up to, say, the sixth order) of the wavefront errors without influencing the Zernike coefficients.¹³ The ocular aberrations can be arranged in a pyramid-like manner with aberrations of the same order on the same level.¹²

Mathematically, the calculation of means is important. With the exception of piston (a lower and zero order aberration), all Zernike polynomials have an average of zero and the average of the entire ocular wavefront should equal the Zernike coefficient of piston .¹³

Wavefront aberrations can be further classified based on their Zernike order as lower (n ≤ 2) or higher order aberrations, with lower order aberrations extending from the zero to the second order, whilst the higher order aberrations (n ≥ 3) are all those above the second order. Both the lower and higher order ocular aberrations affect the visual performance of an individual.

Lower order aberrations (LOA) are sub-categorised as zero, first and second order aberrations. The zero order aberration is singular in nature and is termed piston . It can be described as the forward or backward shift of the entire wavefront; piston does not have an impact on the shape of the wavefront and is often not measured by typical wavefront sensors.¹⁴ First order aberrations include x-tilt and y-tilt and, as the terms suggests represent the tipping or tilting of the wavefront around the x-(horizontal) or y-(vertical) axis.⁷

The classification of refractive error is needed in the clinical practice of all eye care practitioners as well as a baseline for many research studies that involve different methods of determining refractive errors.¹⁰ Uncompensated refractive error affects people globally and has been classified as the second largest cause of preventable blindness after cataracts as well as the leading cause of visual impairment in school-age children.¹⁵

Refractive error can be described as the target vergence required at the corneal plane to ensure a clear and focused image on the retina.¹⁰ Refractive error, in terms of clinical notation, is cited as sphere, cylinder and corresponding axis. In relation to wavefront abberometry, refractive error can be determined through the second order aberrations,¹⁶ these aberrations being spherical defocus, x-astigmatism and y-astigmatism ¹⁶ Spherical defocus is related to the spherical ametropia found in the refractive error, either the hyperopic or myopic entity in the clinical representation of the prescription. Spherical defocus describes the position of the image formation in a purely spherical manner in relation to the retina.

The x- and y-astigmatism, commonly known solely as astigmatism, is the refractive condition whereby the eye cannot produce a point image and the astigmatic refractive error varies in the different meridians.¹⁷ There is a method available for combining x- and y-astigmatism into one term for simplicity, instead of separately representing it as x- and y-components.¹⁸ Combined astigmatism of the x and y variety can be joined and represented by a single surface. Therefore one can combine the x- and y- Zernike polynomials into a single term,¹⁸ which can be achieved using two equations: one to determine a new angle whilst the other is used to determine the combined Zernike coefficient of the x- and y-astigmatism.¹⁸

Second order aberrations, since they are related to refractive error, usually can be easily alleviated by prescribing compensatory spectacles or contact lenses, or by refractive surgery.^10,16

In optometric practice, second order aberrations are the most important and the most clinically significant of the lower order aberrations. There are several ways to represent second order aberrations in terms of refractive error, either clinically (clinical prescription, in terms of sphere and cylinder power with a corresponding axis) or mathematically (using matrices and symmetric dioptric power spaces). The dioptric power space allows the clinical prescription of sphere (F_s), cylinder (F_c) and axis (A) to be displayed as a 2 x 2 matrix using Keating’s equations below:¹⁹

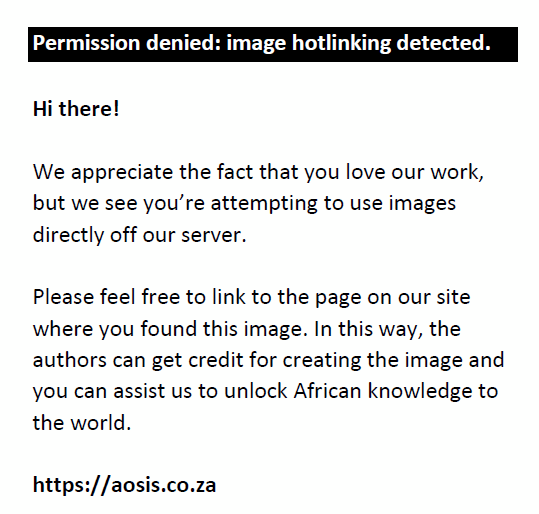
and

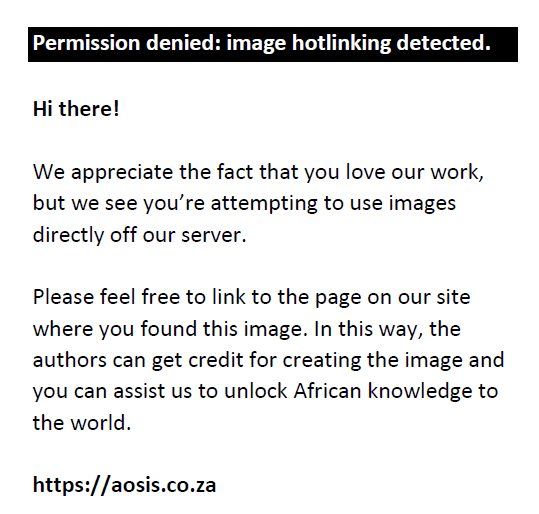
Where

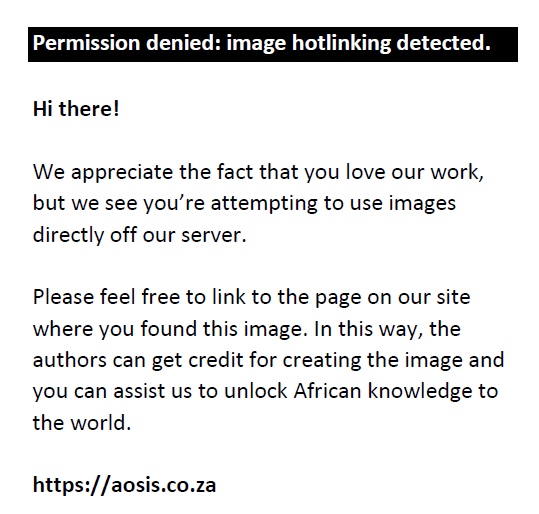
The wavefront aberrometer has the ability to display the second order aberrations as the above-mentioned Zernike coefficients. If one wishes to, these Zernike coefficients, measured in micrometers (µm), can be converted to the clinical notation using the multiple equations below,¹³ where R is the radius of the pupil at the time of the measurement:

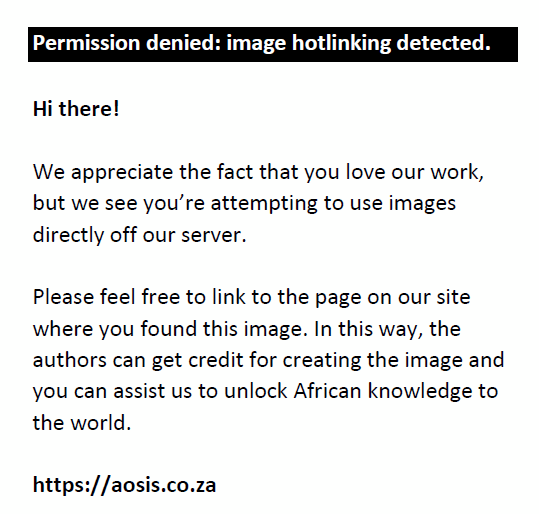
and

Higher order aberrations (HOA) are all those aberrations that fall within the third order and above. These aberrations can negatively affect the vision of seemingly healthy eyes and typically cannot be easily corrected with non-invasive procedures or devices such as spectacles and contact lenses.⁷ Higher order aberrations prompted interest after patients who had received treatment for refractive error by means of refractive surgery, still complained of visual disturbances, especially under scotopic conditions.

The cornea is the primary refracting surface of the ocular system. As the cornea contributes to most of the refracting power of the eye, it stands to reason that aberrations will be more severe if the cornea is distorted.²⁰ An increase in higher order aberrations often occurs after refractive surgery, and results from the change to the corneal surface.

Third order aberrations include x- and y- trefoil as well as x- and y- coma. Trefoil and coma are both classified as a form of irregular astigmatism which results in an irregular or distorted wavefront.⁷

The number of aberrations per order increases as the order of the Zernike polynomials increases. In the fourth order there are five types of aberrations namely: x- and y- quatrefoil, x- and y- secondary astigmatism and spherical aberration .¹³ Quatrefoil and secondary astigmatism are also classified as forms of irregular astigmatism; and the more distorted the wavefront with astigmatism, the more complex the mathematics behind the wavefront error becomes.⁷

Spherical aberration is often caused by the difference in refracting power of the lenticular annular rings of the internal crystalline lens as well as the pupil size.⁷ The larger the pupil diameter, the greater the influence of paraxial light on the peripheral annular zones of the lens. Peripheral light is refracted to a greater or lesser extent and is therefore focused off the retina, causing visual disturbances.²¹ Spherical aberration produces a wavefront with uniform curvature in the center of the pupil; however, the curvature of the wavefront becomes irregular as one examines the more peripheral areas of the pupil, which creates a concentric ring pattern. Pupillary miosis can cause a decrease in the effects of spherical aberration as less of the peripheral lenticular rings are exposed to incident light.⁷ Spherical aberration can also be influenced by those factors that influence the lens, such as accommodation and age.⁷ Individual variation amongst patients and results is common. It has been reported that Zernike coefficients can vary from -0.579 micrometers to 0.572 micrometers for spherical aberration.²⁰

Ocular higher order aberrations can be expanded as far as the instrument will allow in terms of order. However, those of main interest are the third and fourth orders, as the fifth and sixth order aberrations are usually very small in magnitude and therefore negligible.²² Whilst all higher order aberrations can affect vision negatively, the two that are most likely to impinge on visual performance are coma and spherical aberration.⁷

Coma, as mentioned above, is a form of irregular astigmatism. The wavefront produced when coma is present is asymmetrical and the image created on the retina has a comet-like or flare-like appearance.⁷ Coma exists because of misalignment of the centres of the pupil, cornea and lens. The presence of a large amount of coma during aberration measurements has been seen to relate to progressive corneal eye diseases, such as keratoconus.⁷

Spherical aberration presents as complaints of halos and night vision disturbances owing to the lenticular annular zones and enlarged pupil diameter during dim lighting conditions.⁷ It has been suggested that the crystalline lens is liable for a large portion of all internal aberrations present in the eye.²² Owing to the nature and function of the lens, it is understandable that accommodation would influence spherical aberrations. While the ocular accommodation system is relaxed, spherical aberration is usually positive. As accommodation increases between two and three diopters,²³ spherical aberration decreases and becomes less positive or even negative. The change in spherical aberration as accommodation increases can be explained as resulting from the shape and position variation of the ocular lens.^23,24 Spherical aberration is challenging to correct as any spectacle lens compensation only corrects the spherical aberration in the pupil centre whilst the remaining peripheral rings of aberration can continue to cause visual disturbances.²³

Wavefront aberrations represented with Zernike polynomials and coefficients can be difficult to understand and interpret, and therefore the root mean square (RMS) can be valuable when assessing the wavefront error.²⁵ The RMS is calculated using the differences between the wavefront surface and the average or mean of the said surface; this allows the wavefront error (wfe) to be represented as a single number that is more straightforward and easily interpreted.²⁵ In simpler terms, RMS_wfe is the deviation of the wavefront from a plane wavefront represented as a single digit.¹³

RMS_wfe can be calculated using the information given by the aberrometer once a measurement has been taken.²⁵ The RMS can be determined individually for lower or higher order aberrations or it can be calculated for the entire wavefront.¹³ The RMS can be calculated using the Zernike coefficients as shown in the equation below using the single indexing system:¹³

As seen in the above equation, piston is not included in the calculation as it has no effect on the quality of the retinal image.¹³ The Zernike coefficients are measured in micrometers (μm) and therefore it follows that RMS_wfe is also recorded in the same unit.¹³ Whilst RMS_wfe assists in interpreting wavefront error, it is not directly correlated to visual performance, as different aberrations do not affect visual performance equally.²⁶

Refractive surgery has become increasingly popular for the correction of unwanted refractive errors. The surgery aims to eliminate the presence of lower order aberrations, namely defocus and x- and y-astigmatism. Whilst most surgical interventions are successful in reducing or eradicating refractive errors, patients still present with visual disturbances.

The development of wavefront aberrometers has allowed the thinking that higher order aberrations can also be corrected in time with refractive surgery via custom ablation or custom contact lenses. There are, however, already limitations to this notion. With current wavefront analysers, the ability to reproduce wavefront measurements that are reliable has not yet been done successfully. Wavefront aberrations are seen to be dynamic which poses a problem for correction.

Refractive surgery, however, has been shown to increase higher order aberrations, often because of the induced corneal changes²⁰ and particularly causes an increase in coma and spherical aberration. The symptoms that can present after refractive surgery include glare, halos, poor scotopic (night) vision, decreased contrast sensitivity and poor subjective refraction results.²⁷ The causes of glare and halos include an increase in scattered light entering the eye, an increase in spherical aberration and coma, and corneal surface defects as a result of the surgery.²⁸

The increase in scattered light usually results from the size of the ablation zone chosen during surgery. Light will strike the cornea as well as the edge of the ablation zone, and this causes increased scattering of light and therefore becomes the source of the visual disturbance. Constriction of the pupil should in theory decrease the amount of light scattered.²⁸

Spherical aberration has also been seen to increase after ablation refractive surgery. As mentioned above, spherical aberration is responsible for the presence of glare and halos, and therefore the increase in spherical aberration after refractive surgery would result in a heightening of these visual disturbances.²⁸ The amount and sign of spherical aberration differs for different refractive states. Myopic ablation patterns tend towards positive spherical aberrations whilst hyperopic ablation patterns are more negative.²⁹

Refractive surgery causes changes to the corneal surface and can therefore induce unwanted aberrations. Striae or folds within the cornea can add to the increase in experienced glare and halos.²⁸

Pre-operative higher order RMS_wfe values provide surgeons with an indication as to which aberrations may increase after surgery. The smaller the higher order RMS_wfe before surgery, the more likely that the procedure will increase aberrations post-operatively.¹³

The discovery of an increase in higher order aberrations after refractive surgery has contributed to the development and advancements in laser ablation technology during refractive surgery. In attempts to decrease the induced higher order aberrations after surgery, ophthalmic surgeons have begun using wavefront-guided excimer laser refractive surgery.²⁰ This form of surgery was introduced in the year 2000 ²⁰ to decrease or eliminate total aberrations of the eye and not focus individually on lower or higher order aberrations.²⁰ The principle behind this new technology was to take measurements using a wavefront aberrometer and use the results to create an ablation pattern that effectively neutralises existing aberrations.²⁰

A study was conducted on three eyes of patients who had already received wavefront-based custom corneal ablation.³⁰ The study found that an unaided visual acuity of 6/3 was found in two of the three eyes whilst the remaining eye had better than 6/6 visual acuity. The wavefront deviations were also found to have decreased by 27%. In another study, 93.5% of patients had an unaided visual acuity of 6/6 or better.³⁰

Whilst this method has not been perfected owing to the existence of external variables such as ablation zone placement, cyclotorsion of the eye and wound healing, this type of surgery is proving to provide patients with improved post-operative vision.²⁸

With the advancement of technology, it has become possible to alleviate a patient’s refractive error with the help of refractive surgery. However, with the induction of higher order aberrations post-operatively, patients are occasionally visually disadvantaged after having received surgery. With this discovery, newer technology is developing using wavefront-guided laser ablation to ensure that minimal aberrations are induced and that pre-existing aberrations are neutralised. Wavefront aberrations are, however, important for many reasons other than refractive surgery; for example, changes in aberrations owing to disease are vital for proper diagnosis and management for some patients. The influences of cycloplegia on ocular aberrations is another area of interest that will be described in future papers by the present authors.

The authors declare that they have no financial or personal relationships which may have inappropriately influenced them in writing this article.

This article results from preliminary research towards a MPhil degree in optometry undertaken by H.A.U. (University of Johannesburg) with the supervision of A.R. (University of Johannesburg).

1. Nam J, Thibos LN, Iskander DR. Describing ocular aberrations with wavefront vergence maps. Clin Exp Optom. 2009;92:194–205. http://dx.doi.org/10.1111/j.1444-0938.2009.00358.x
2. Cade F, Cruzat A, Paschalis EI, Santo LE, Pineda R. Analysis of four aberrometers for evaluation lower and higher order aberrations. Public Lib Sci ONE. 2013;8:1–7.
3. Lin HZ, Chen C, Lee Y. Effect of pharmacologic pupil dilation with tropicamide and phenylephrine on wavefront measurements. Taiwan J Ophthal. 2013;3:62–66. http://dx.doi.org/10.1016/j.tjo.2013.03.002
4. Salmon TO, Van de Pol C. Evaluation of a clinical aberrometer for lower-order accuracy and repeatability, higher-order repeatability, and instrument myopia. Optom. 2005;76:461–472. http://dx.doi.org/10.1016/j.optm.2005.07.006
5. Hiraoka T, Yamamoto T, Okamoto F, Oshika T. Time course of changes in ocular wavefront aberration after the administration of eye ointment. Eye. 2012;26:1310–1317. http://dx.doi.org/10.1038/eye.2012.142
6. Collins MJ, Buehren T, Bece A, Voetz SC. Corneal optics after reading, microscopy and computer work. Acta Ophthalmol Scand. 2006;84:216–224. http://dx.doi.org/10.1111/j.1600-0420.2005.00547.x
7. Yanoff M, Duker JS. Ophthalmology. 3rd ed. Beijing: Elsevier Heath Sciences, 2009; p. 33, 53, 132, 166.
8. Arines J, Pailos E, Prado P, Bará S. The contribution of fixational eye movements to the validity of the measured ocular aberration. Ophthal Physiol Opt. 2009;29:281–287. http://dx.doi.org/10.1111/j.1475-1313.2009.00663.x
9. Comastri SA, Martin G, Pfortner T. Analysis of pupil and corneal wave aberration data supplied by the SN CT 1000 topography system. Optik. 2005;117:537–545. http://dx.doi.org/10.1016/j.ijleo.2005.11.018
10. Martin J, Vasudevan B, Himebaugh N, Bradley A, Thibos L. Unbiased estimation of refractive state of aberrated eyes. Vis Res. 2011;51:1932–1940. http://dx.doi.org/10.1016/j.visres.2011.07.006
11. Barnes- Svarney P. The handy math answer book. Michigan: Visible Ink Press, 2000; p. 150.
12. Jagerman LS. Ophthalmologists, meet Zernike and Fourier. British Columbia: Trafford Publishing, 2007; p. 9, 34, 53.
13. Dai G. Wavefront optics for vision correction. Washington: SPIE Press, 2008; p. 26, 43–53, 61, 264. http://dx.doi.org/10.1117/3.769212
14. Geary JM. Introduction to wavefront sensors. Washington: SPIE Press, 1995; p. 27. http://dx.doi.org/10.1117/3.179559.ch3
15. Sharma A, Congdon N, Patel M, Gilbert C. School-based approaches to the correction of refractive error in children. Surv Ophthalmol. 2012;57:272–283. http://dx.doi.org/10.1016/j.survophthal.2011.11.002
16. Koury JB. Wavefront and emerging refractive technologies. Netherlands: Kugler Publications, 2003; p. 9.
17. Grosvenor TP. Primary care optometry. 5th ed. Missouri: Butterworth Heinemann Elsevier, 2007; p. 199.
18. Campbell CE. A new method for describing the aberrations of the eye using Zernike polynomials. Optom Vis Sci. 2003;80:79–83. http://dx.doi.org/10.1097/00006324-200301000-00011
19. Keating MP. An easier method to obtain the sphere, cylinder and axis from an off-axis dioptric power matrix. Am J Optom Physiol Opt. 1980;57:734–737. http://dx.doi.org/10.1097/00006324-198010000-00007
20. Agarwal A, Agarwal A, Jacob S. Refractive surgery. 2nd ed. New Delhi: Jaypee Brothers Publishers, 2009; p. 152–154. http://dx.doi.org/10.5005/jp/books/10723
21. Agarwal S, Agarwal A, Buratto L, Apple DJ, Ali JL. Textbook of ophthalmology. New Dehli: Jaypee Brothers Publishers, 2002; p. 136.
22. Phillip K, Martinez A, Ho A, et al. Total ocular, anterior corneal and lenticular higher order aberrations in hyperopic, myopic and emmetropic eyes. Vis Res. 2012;52:31–37. http://dx.doi.org/10.1016/j.visres.2011.10.018
23. Thibos LN, Bradley A, López-Gil N. Modelling the impact of spherical aberration on accommodation. Ophthal Physiol Opt. 2013;33:482–496. http://dx.doi.org/10.1111/opo.12047
24. Buehren T, Collins MJ, Loughridge J, Carney LG, Iskander DR. Corneal topography and accommodation. Cornea. 2003;22:311–316. http://dx.doi.org/10.1097/00003226-200305000-00007
25. Bille JF, Harner CFH, Lösel F. Aberration-free surgery: New frontiers in vision. Heidelberg: Springer, 2004; p. 7–8. http://dx.doi.org/10.1007/978-3-642-18161-0
26. Vinciguerra P, Camesasca FI. Refractive surface ablation: PRK, LASEK, Epi-LASEK, Custom, PTK and retreatment. New Jersey: SLACK Incorporated, 2007; p. 22.
27. Li B, Wang Z, Wang W, Liu M, Quan W. Effects of interaction among wave aberrations on optical image quality after refractive surgery. Optik. 2010;121:127–131. http://dx.doi.org/10.1016/j.ijleo.2008.05.023
28. Agarwal A. Refractive surgery nightmares: Conquering refractive surgery catastrophes. New Jersey: SLACK Incorporated, 2007;p. 37–38.
29. Alió JL, Pinero D, Muftuoglu O. Corneal wavefront-guided retreatments for significant night vision symptoms after myopic laser refractive surgery. Am J Ophthalmol. 2008;145:65–74. http://dx.doi.org/10.1016/j.ajo.2007.08.025
30. Davies N, Diaz-Santana L, Lara-Saucedo D. Repeatability of ocular wavefront measurement. Optom Vis Sci. 2003;80:142–150. http://dx.doi.org/10.1097/00006324-200302000-00010